【摘 要】为了降低计算容量衰减系数时的误差，优化电池容量配置结果，提高电池容量，本研究设计了储能站的电池精细化配置方法：首先，分别设计最大波动函数、电能最大函数值和电池储能容量的目标函数；其次，基于目标函数建立荷电状态下的初始电能输出功率以及额定容量的约束条件；再次，建立储能站电池容量衰减模型，降低电池容量衰减过程中的计算误差；最后，设计电池容量配置算法，简化衰减模型，依据荷电状态计算各阶段的斜率指标，获得衰减系数，实现电池容量的精细化配置。实验结果表明，应用本研究设计的储能站的电池精细化配置方法，电池最大容量有效提高，达到33 MWh，具备较好的电池容量配置优化效果，更好地起到“削峰填谷”的作用，增强了储能站对电力系统的调节能力。

【关键词】储能电站；电池；精细化；配置方法；容量衰减模型；容量配置算法

引言

目前储能站中的储能设备具备一定的局限性，在容量方面，还具备较大的提升空间，因此，对电池的配置形式进行优化至关重要[1]。本研究在总结以往成果的基础上，提出了储能站的电池精细化配置方法：设计最大波动函数、电能最大函数值和电池储能容量的目标函数；建立荷电状态下的初始电能输出功率以及额定容量的约束条件；基于目标函数和约束条件，建立储能站电池容量衰减模型，降低电池容量衰减过程中的计算误差；创新性地设计电池容量配置算法，分段处理电池负荷，简化衰减模型，依据荷电状态计算各阶段的斜率指标获得衰减系数，求解模型的功率和容量配置最优解，从而实现电池容量的精细化配置。

一、电池精细化配置方法设计

（一）电池储能系统目标函数和约束条件

在储能站的电池储能功率中，功率波动需要满足一定的函数需求。设功率波动差值如式（1）所示：

ΔWo =Wo（ t ）−Wo（ t −1） （1）

式（1）中，ΔWo 为蓄电池内功率波动的上限与下限之差，Wo（t） 为时间t 时内的电池输出功率，Wo（t－1） 为t 时刻的前一时刻的电池输出功率[2-3]；依据功率波动差值，可以得到功率的最大波动函数：

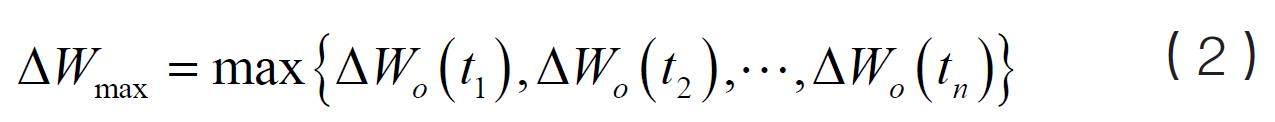
式（2）中，ΔWmax 为储能站中蓄电池输出功率波动的最大函数值[4-5]；基于该函数值，可以计算一段时间内功率的变化率，如式（3）所示：

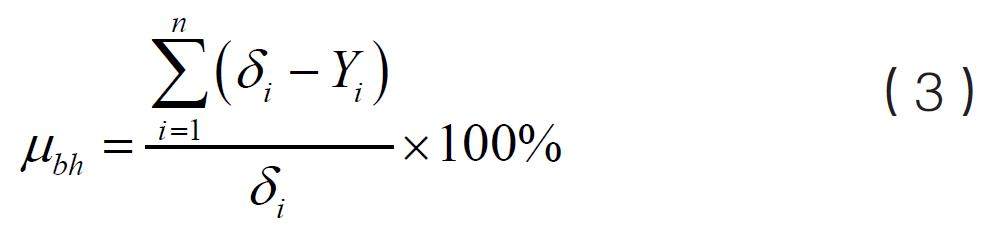
式（3）中，μbh 为i 时刻时蓄电池输出功率的变化率，δi为i 时刻前功率输入的变化量，Yi 为i 时刻后功率输入的变化量，据此得到一段时间内输入功率变化量的最大值，如式（4）所示：

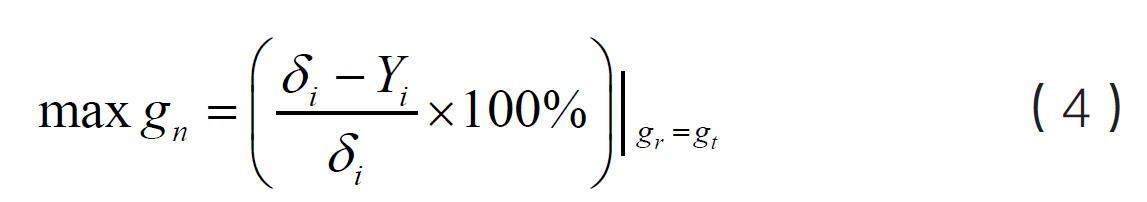
式（4）中，gn 为电池电能输入的最大函数值，gr 为当前频率的高频波动分量，gt 为当前时间的频率波动；在结合以上电池功率变化及波动的函数后，可以得到电池储能容量的目标函数优化结果，如式（5）所示：

式（5）中，Pyu 为分布式能源下电池管理系统的配置频率，Gte 为电池储能系统的最大功率，Rs（Pyu ，Gte） 为综合分布式能源以及储能站系统的容量最优配置，fj 为电池的各项储能功率配置，gj 为电池的单位功率调节系数，fi 为能量型的电池管理电压，Hb 为系统的整体数量[6]；结合以上目标函数，假设电能的荷电初始状态为Yg，可以得到某时刻的荷电状态，如式（6）所示：

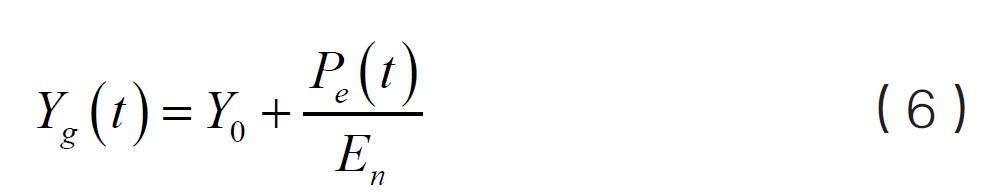
式（6）中，Yg（t） 为t 时刻时电池储能的荷电状态所能够保持的电量，Y0 为蓄电池中的荷电状态，Pe（t） 为t 时刻电池储能功率，En 为能量稳定运行的状态下采样周期内的输出功率期望值。